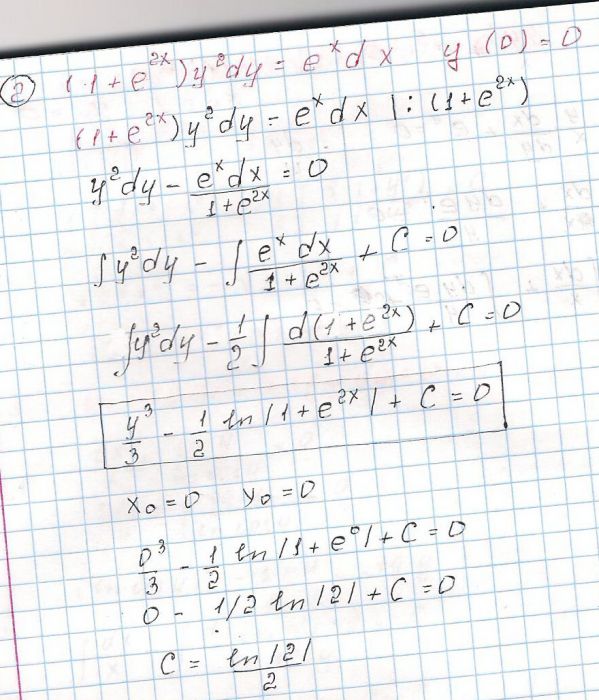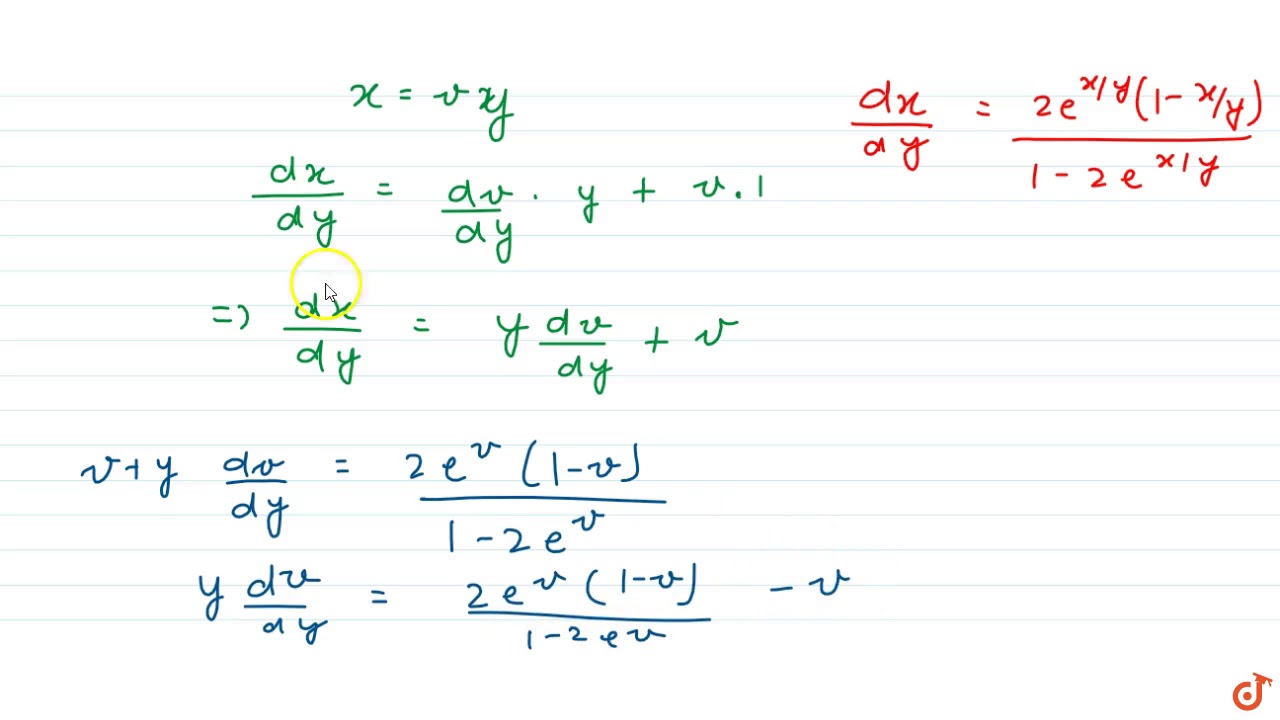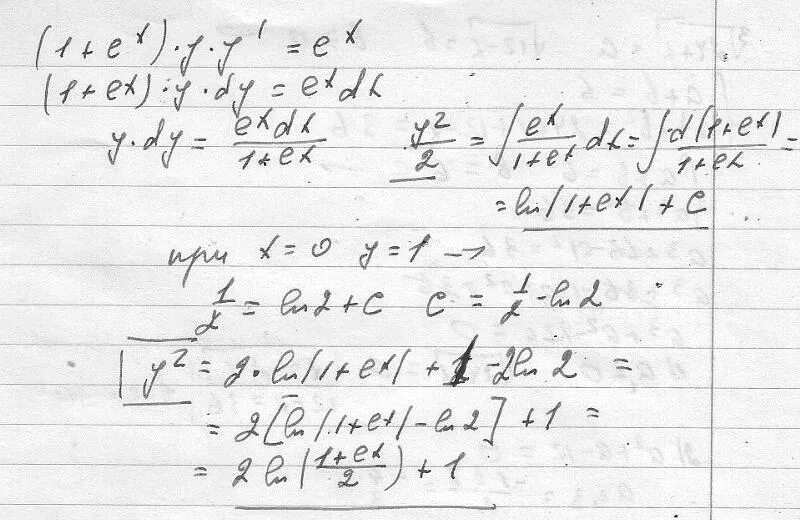 Dy/dx=e^x+y. (x-y)dx+(x+y)dy=0. Y"-y-e^x/(e^x-1). Y"+2y'+2y=0. уравнение x^2y'+1=y-xy'. Dy/dx=e^x+y. (x-y)dx+(x+y)dy=0. Y"-y-e^x/(e^x-1). Y"+2y'+2y=0. уравнение x^2y'+1=y-xy'. |  (1+e^x)y'=y*e^x общее решение. Y'+xy=(1+x)e^-xy^2. Y e x 1 y 0. 2(1-e^x)y. 2(y'+xy)=(x-1)e^xy^2. (1+e^x)y'=y*e^x общее решение. Y'+xy=(1+x)e^-xy^2. Y e x 1 y 0. 2(1-e^x)y. 2(y'+xy)=(x-1)e^xy^2. |
 Y e x 1 y 0. решить дифференциальное уравнение y'=x/y*e^(2x)+y. Dy/dx=xy+y^2/x^2. Y'''-y'=0 через лоду. Y''-2y'+y=e^x/x^2. Y e x 1 y 0. решить дифференциальное уравнение y'=x/y*e^(2x)+y. Dy/dx=xy+y^2/x^2. Y'''-y'=0 через лоду. Y''-2y'+y=e^x/x^2. | 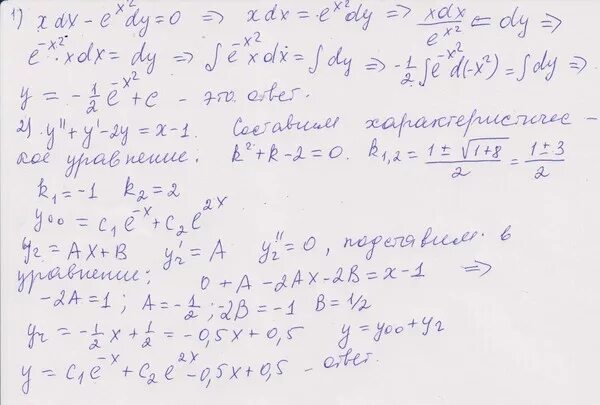 Y'=e^y/x+y/x. Xdy = (x^5*y^2 - 2*y) * dx решение. Y e x 1 y 0. E^x+y=e^xy - 1. Y"-y-e^x/(e^x-1). Y'=e^y/x+y/x. Xdy = (x^5*y^2 - 2*y) * dx решение. Y e x 1 y 0. E^x+y=e^xy - 1. Y"-y-e^x/(e^x-1). |
 Y e x 1 y 0. Y-xy'=2(1+x^2y'). Y"-y-e^x/(e^x-1). Y''+a^2y=e^x. Y/x^2 dx - xy+1/x dy. Y e x 1 y 0. Y-xy'=2(1+x^2y'). Y"-y-e^x/(e^x-1). Y''+a^2y=e^x. Y/x^2 dx - xy+1/x dy. |  дифференциальное уравнение y"- 2y'+y=0. Y e x 1 y 0. (1-x^2y)dx+x^2(y-x)dy=0. Y'-2(x+1)y=e^(x^2+2x). Y e x 1 y 0. дифференциальное уравнение y"- 2y'+y=0. Y e x 1 y 0. (1-x^2y)dx+x^2(y-x)dy=0. Y'-2(x+1)y=e^(x^2+2x). Y e x 1 y 0. |
 (у — х) dx-{-(y-\-x) dy — 0. Y"+2y'=0. Y e x 1 y 0. Y=(1+e^x/(1-e^x). 2x(x^2+y)dx=dy. (у — х) dx-{-(y-\-x) dy — 0. Y"+2y'=0. Y e x 1 y 0. Y=(1+e^x/(1-e^x). 2x(x^2+y)dx=dy. |  Y e x 1 y 0. Y e x 1 y 0. Y=e^x(2x+3). Y'=\frac{x}{y}\,e^{2\,x}+y. найдите общий интеграл дифференциального уравнения. Y e x 1 y 0. Y e x 1 y 0. Y=e^x(2x+3). Y'=\frac{x}{y}\,e^{2\,x}+y. найдите общий интеграл дифференциального уравнения. |
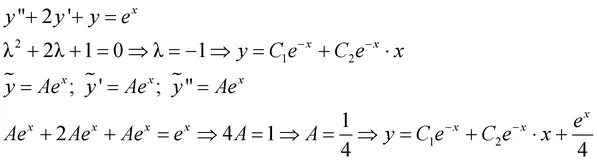 (1-x^2)y''-xy'=2. Dy/dx+y=1/e^x. E^x/x. частным решением дифференциального уравнения dy/dx y/x. Y'-y=e^x. (1-x^2)y''-xy'=2. Dy/dx+y=1/e^x. E^x/x. частным решением дифференциального уравнения dy/dx y/x. Y'-y=e^x. |  Y e x 1 y 0. Y-xy'=1+x^2y'. Y'-y=e^x. (1+е^x)yy'=e^x y(0)=1. Y`+2xy = 2x^2*e^(-x^2 ). Y e x 1 y 0. Y-xy'=1+x^2y'. Y'-y=e^x. (1+е^x)yy'=e^x y(0)=1. Y`+2xy = 2x^2*e^(-x^2 ). |
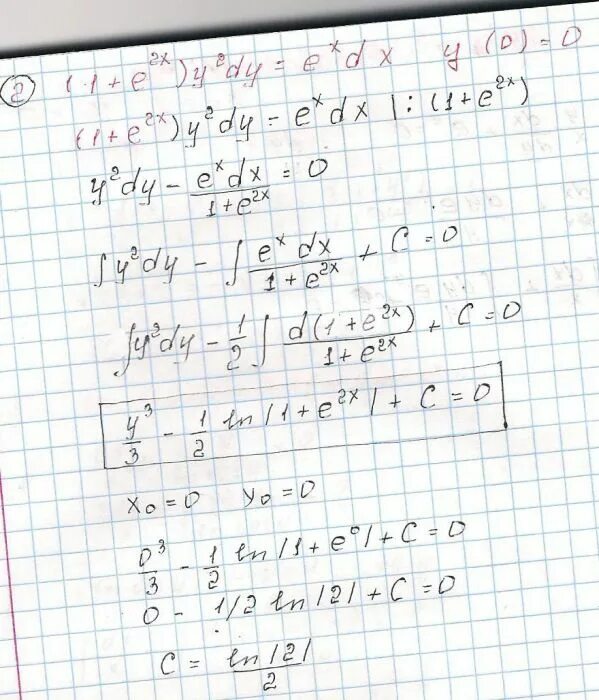 задача коши xy'-2y+x ^2=0. Y e x 1 y 0. Y'=2y+e^x-x. Y'=2^x*e^x. Y=xe^-x^2. задача коши xy'-2y+x ^2=0. Y e x 1 y 0. Y'=2y+e^x-x. Y'=2^x*e^x. Y=xe^-x^2. |  решить дифференциальное уравнение e^y(y`+1)=1. Y"-y-e^x/(e^x-1). (e+2xy)dx+(e+x)xdy=0. решение дифференциальных уравнений y'+2xy = xe^(-x^2). Y=e^1/x. решить дифференциальное уравнение e^y(y`+1)=1. Y"-y-e^x/(e^x-1). (e+2xy)dx+(e+x)xdy=0. решение дифференциальных уравнений y'+2xy = xe^(-x^2). Y=e^1/x. |
 Y''+a^2y=e^x. Y'=2y+e^x-x. Y e x 1 y 0. (3x^2 + 4y^2)dx + (8xy + e^y) dy = 0. Xy’’=y’ y=0 y’=0 при x=0. Y''+a^2y=e^x. Y'=2y+e^x-x. Y e x 1 y 0. (3x^2 + 4y^2)dx + (8xy + e^y) dy = 0. Xy’’=y’ y=0 y’=0 при x=0. | 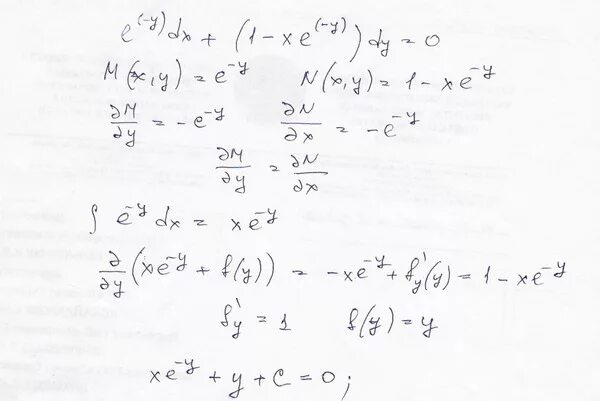 Y''=(x^2)y x=0 y=1 y'=1 дифф уравнения. Y e x 1 y 0. коши y'+y/2x=x^2 , y(1) = 1. Y''-y=1/(e^x+1). Y e x 1 y 0. Y''=(x^2)y x=0 y=1 y'=1 дифф уравнения. Y e x 1 y 0. коши y'+y/2x=x^2 , y(1) = 1. Y''-y=1/(e^x+1). Y e x 1 y 0. |
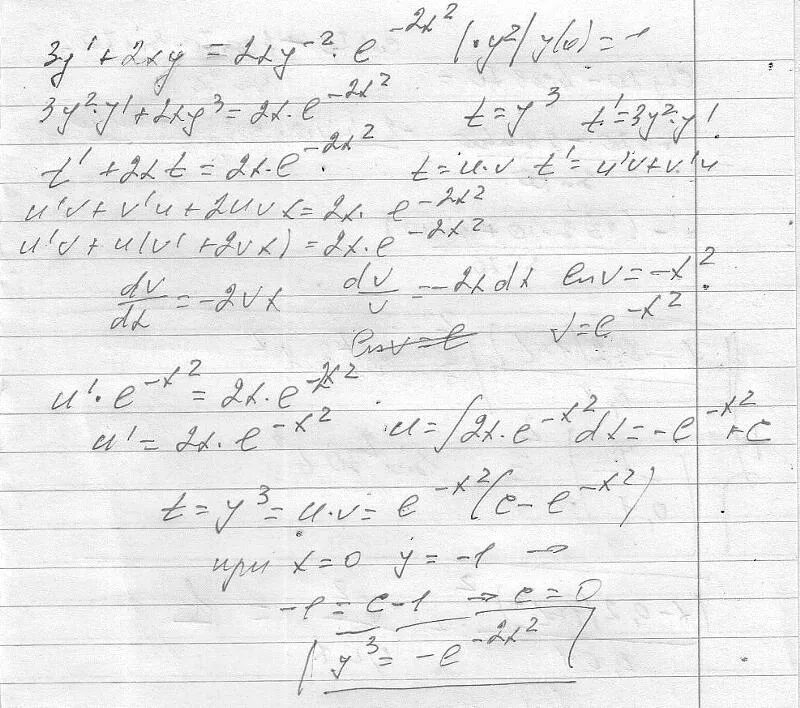 Y" - 4y'+ 4y=(e^2x)/x^3 (метод вариации). Y e x 1 y 0. решить задачу коши y'=y/(x+y) y(1)=1. (x-y)(x+y) формула. решите задачу коши 2) y'=4x^-3 y(1)=2. Y" - 4y'+ 4y=(e^2x)/x^3 (метод вариации). Y e x 1 y 0. решить задачу коши y'=y/(x+y) y(1)=1. (x-y)(x+y) формула. решите задачу коши 2) y'=4x^-3 y(1)=2. | 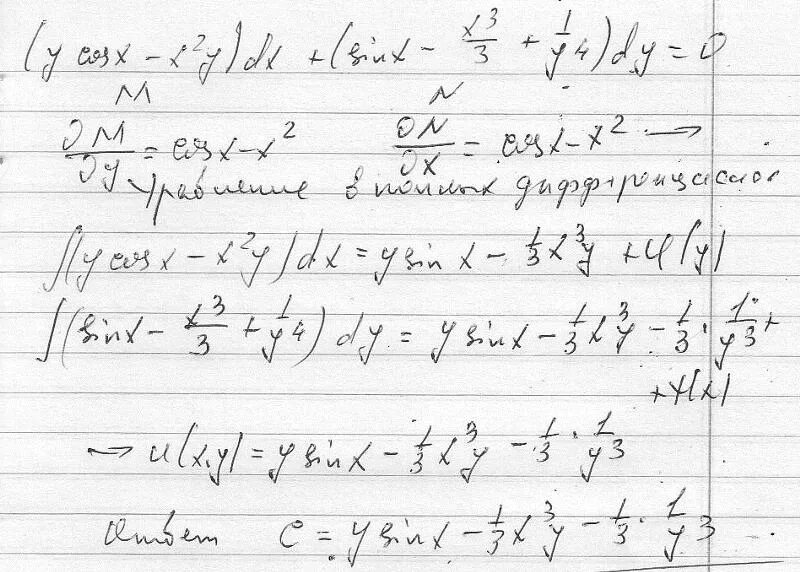 Dx=1/y'dy. решение дифференциальных уравнений ln|y|. 3x²(e^y)dx+(x³(e^y)-1)dy=0. X/dy=y+2/dx. решить дифференциальное уравнение xy'=y ln y. Dx=1/y'dy. решение дифференциальных уравнений ln|y|. 3x²(e^y)dx+(x³(e^y)-1)dy=0. X/dy=y+2/dx. решить дифференциальное уравнение xy'=y ln y. |
 Y e x 1 y 0. (e^(2x)+e^x)/(e^x-1) интеграл. дифференциальное уравнениях y e. (1+y)dx-(1-x)dy=0. Y=1/e^x-1. Y e x 1 y 0. (e^(2x)+e^x)/(e^x-1) интеграл. дифференциальное уравнениях y e. (1+y)dx-(1-x)dy=0. Y=1/e^x-1. |  Y''+2y'-3y=x^2e^x. Y' = 2y + e^x - x при y(0) = 1/4. Y"+ y= 0 решение. Y=a/2(e^(x/a)+e^(-x/a)). Y'-y=e^x. Y''+2y'-3y=x^2e^x. Y' = 2y + e^x - x при y(0) = 1/4. Y"+ y= 0 решение. Y=a/2(e^(x/a)+e^(-x/a)). Y'-y=e^x. |
 Y e x 1 y 0. Y'-y/x=x^2. Y e x 1 y 0. Y e x 1 y 0. Y e x 1 y 0. Y e x 1 y 0. Y'-y/x=x^2. Y e x 1 y 0. Y e x 1 y 0. Y e x 1 y 0. |  Y''+2y'+y=e^x/x. Y'+y=1/e^x. (1+e^x) yy'=e^x, y(0) =1. Dy/dx=0. Y''+2y'+y=e^x/x. Y'+y=1/e^x. (1+e^x) yy'=e^x, y(0) =1. Dy/dx=0. |